Aversive/Modules/devices/control system/filters

Generic Filter Interface

This is the minimal interface of a digital discrete filter. The filter is organized to be usable in multiple instances, and can be directly called by the Control System, in order to act as a control loop.

struct example_filter
{
   .... /* internal variables needed by the filter */
};

This structure stores the internal variables of the filter. The elements of this struct should only be acessed via accesor functions. The pointer to this struct will be passed to all functions for using the filter.

void example_init(struct pid_filter * p);

This function initializes the values in the structure

s32 example_do_filter(struct pid_filter * p, s32 in);

This function exectes one iteration of the filter. Input and output values are passed.

Biquad

This filter is a general IIR digital filter. All IIR and FIR filters can be implemented using this module. For details, see Biquad doc and design procedure

The quadramp can also be used as general purpose integration, or derivation , or simply a coefficient!!

This provides a convenient way to implement this simple functions when you need them in a feedback filter, for example.

PID

Description

This module is a simple implementation of a PID. It is done in the parallel implementation. The PID is of course, intended as a correction filter (loop filter), not as a return or consign filter.

There are saturations of different variables available. The most important saturation is the saturation of the integral memory. Without this, the algorithm can overflow when a mecanical blocking occurs.

Structures

struct pid_filter
{
   s16 gain_P; /**< Gain of Proportionnal module */
   s16 gain_I; /**< Gain of Integral module */
   s16 gain_D; /**< Gain of Derivate module */

   s16 out_shift; /**< (XXX) */

   s32 max_in; /**<  In saturation levels */
   s32 max_I; /**<   Integral saturation levels */
   s32 max_out; /**< Out saturation levels */

   s32 integral; /**< previous integral parameter */
   s32 last_in;  /**< previous derivate parameter */
};

Transfer function

T is the recurrence time (time between calls of pid_do_filter() )

• continuous form :

<math>output = $\frac {gain_P * input(t) + gain_I * $\int(input(t), dt) * 1/T + gain_D * d(input(t))/dt * T } { 2^ out_shift }</math>

• Z transform

<math>output = $\frac {gain_P * input + gain_I * input / (1-z^-1) + gain_D * input * (1-z^-1)} { 2^ out_shift }</math>

<math>output = $\frac {gain_P+gain_I+gain_D - (gain_P+2gain_D)* z^-1 + gain_D * z^-2 }{( 1 - z^-1 ) * 2^ out_shift }</math>

Interface

void pid_init(struct pid_filter * p);

Initialises all values. The init value is 1 for prop gain, 0 for others. Saturations are deactivated ( -1) The global divisor is at 1.

s32 pid_do_filter(struct pid_filter * p, s32 in);

Executes one iteration

void pid_set_gains(struct pid_filter * p, s16 gp, s16 gi, s16 gd);

void pid_set_maximums(struct pid_filter * p, s32 max_in, s32 max_I, s32 max_out);

void pid_set_out_shift(struct pid_filter * p, s16 out_shift);

Sets gains, max, and out shift. Out shift is the divisor for the output. With setting a divisor on the output it is possible to use fractionnal coefficients.

Ramp

This filter is a consign filter that generates a ramp with a maximum incline, out of an impulse, or any other shape.

This is useful for example for assuring the continuity of a speed consign, if the input consign can be discontinuous.

Structures

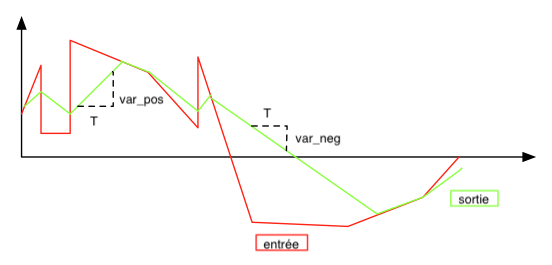
struct ramp_filter {
	u32 var_neg;
	u32 var_pos;
	s32 prev_out;
}

Quadramp

The quadramp module does exactly the same operation than the ramp, but on the derivate of the input. It enshures that the derivate of the output is continuous.

This is useful for generating trajectories while having a continuous speed profile. The speed profile has a trapezoidal shape.

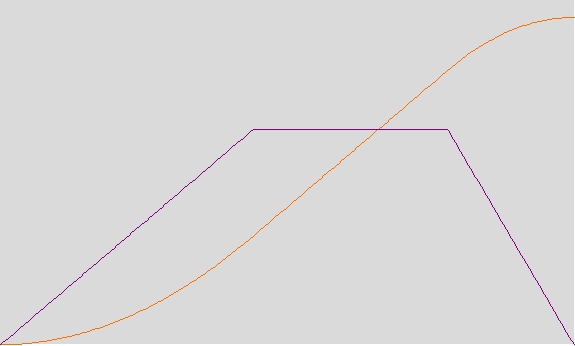
An example of output is given :

Orange : position output

Violet : speed profile ( derivate of the output position)

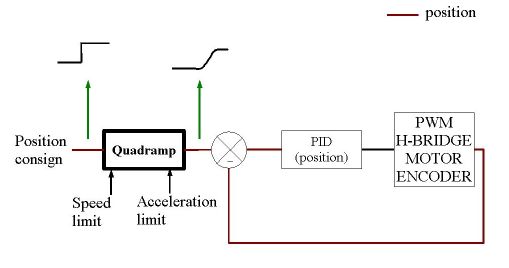
function principle

The functionning principle is shown below

The input is a position consign, which is often changing fast.

you specify then an acceleration and speed limit. These parameters are then used for calculating the trajectory to use, which is then applied to a classical PID (for exemple).

Structures

struct quadramp_filter {
   u32 var_2nd_ord_pos;
   u32 var_2nd_ord_neg;
   u32 var_1st_ord_pos;
   u32 var_1st_ord_neg;

   s32 previous_var;
   s32 previous_out;
}

var_1st_ord_pos et var_1st_ord_neg are the speed limits ( first derivate limit )

var_2nd_ord_neg et var_2nd_ordpos are the acceleration limits ( second derivate limit )

Interface

void quadramp_init(struct quadramp_filter * r);

Initializes all the parameters for an unity filter (values = -1)

s32 quadramp_do_filter(struct quadramp_filter * r, s32 in);

Uses the filter

void quadramp_set_2nd_order_vars(struct quadramp_filter * r, u32 var_2nd_ord_pos, u32 var_2nd_ord_neg);
void quadramp_set_1st_order_vars(struct quadramp_filter * r, u32 var_1st_ord_pos, u32 var_1st_ord_neg);

Accessors to the parameters.

Implementation use

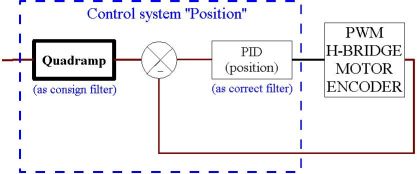
The quadramp is typically used as consign filter in the same CS containing the position PID, as shown below :

Quadramp Derivate

The utility of the quadramp_derivate is very similar to the normal quadramp. Hovewer, the functionnal principle is very different.

Please see the complete documentation